Why does deep and cheap learning work so well?

Lin et al., 2017

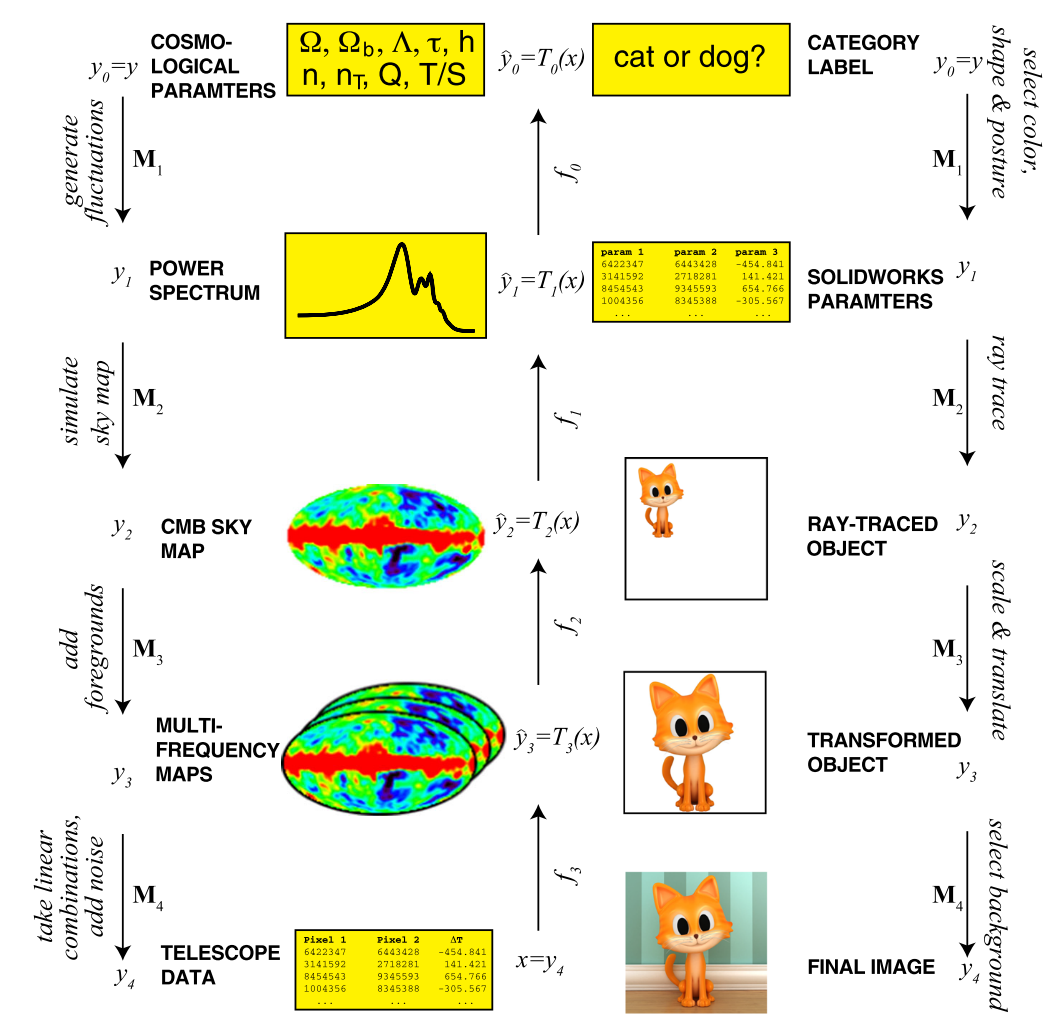Source: Lin et al., 2017

Summary

How do properties frequently encountered in physics (e.g. symmetry, locality, compositionality) translate into simple neural networks?
Show that when data is generated from a common hierarchical form, a deep neural network can be more efficient
- Prove various “no-flattening theorems”
Links: [ website ] [ pdf ]

While the universal approximation theorems prove that neural networks can approximate arbitrary functions well, they do little to explain the empirical efficiency of deep networks
Factors that affect quality of neural networks:
- Expressibility: What class of functions can be expressed?
- Efficiency: How many resources are required to approximate a given function?
- Learnability: How rapidly can the network learn good parameters?
Focuses on expressibility and efficiency by addressing:
How can neural networks approximate functions well in practice, when the set of possible functions is exponentially larger than the set of practically possible networks?
- The fact that networks of feasible size are useful implies the class of functions we care about is dramatically smaller than all possible functions

Interested in probability distribution $p(\textbf{x}|y)$, where $\textbf{x}$ might be the pixels in an image and $y$ the object label (e.g. cat)
Probabilities and Hamiltonians
- Hamiltonian: $H_y(\textbf{x}) \equiv -\ln p(\textbf{x}|y)$
- After some algebra (see paper), $p(\textbf{x}) = \frac{1}{N(\textbf{x})}e^{-\left[\mathbf{H(x)+\mu}\right]}$
- Investigate how well $p(\mathbf{x})$ can be approximated by a neural network
  - $p(\mathbf{x})$ can be obtained by applying softmax layer to $\mathbf{H(x)}$, therefore question becomes how to approximate $\mathbf{H(x)}$ well

Nature favors Hamiltonians that are low-order, sparse, symmetric polynomials – which require few continuous parameters to represent
- Polynomials can be built using multiplications and additions, multiplication can be achieved with four neurons
- Low polynomial order: typically degree ranging from 2 to 4
- Locality: things are only affected by what’s in their immediate vicinity, results in sparsity
- Symmetry: invariance under some transformation (e.g. tranlation or rotation), results in fewer independent parameters
Why deep?
- No-flattening Theorems: Inability of neural networks representing the data from generative processes with hierarchical structure to be efficiently flattened
  - E.g. how matrix multiplication can be optimized by factoring
- Result of the generative process contains much more information than the actual process
  - E.g. “generate a random string of $10^9$ bits”

Success of reasonably sized neural networks hinges on symmetry, locality, and polynomial log-probability in data from the natural world