Scaling Laws for Neural Language Models

Kaplan et al., 2020

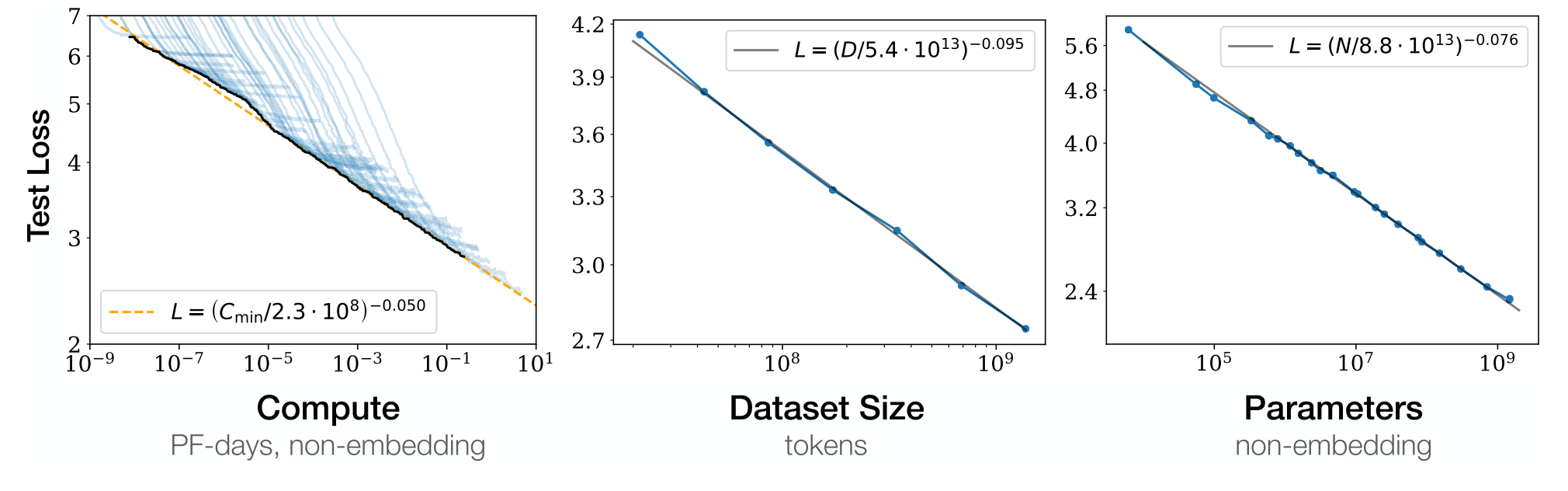Source: Kaplan et al., 2020

Summary

Study empirical scaling laws for language model performance
Loss scales as a power-law with size of model, dataset, and training compute
Architectural details (e.g. network width and depth) have minimal effects
Larger models are significantly more sample-efficient
“…optimal compute-efficient training involves training very large models on relatively modest amount of data and stopping significantly before convergence.”
Links: [ website ] [ pdf ]

While emprically successful, the performance of deep learning models depends on many factors such as model architecture, model size, training compute power, and training dataset size
The high ceiling and low floor performance on language tasks allows for the invesigation of performance trends across several orders of magnitude
Power-law scalings with model and dataset size have been shown in density estimation and random forests

Train (mostly) decoder-only Transformer models on WebText2, web scrape of outbound links from Reddit (20.3M documents, $1.62 \times 10^{10}$ words)
- Fixed $2.5 \times 10^{5}$ steps with batch size of 512 sequences of 1024 tokens
Parameterize Transformer architecture with hyperparameters:
- $n_{l a y e r}$ : number of layers
- $d_{m o d e l}$ : dimension of residual stream
- $d_{f f}$ : dimension of intermediate feed-forward layer
- $d_{a t t n}$ : dimension of attention output
- $n_{h e a d s}$ : number of attention heads per layer
Model size $N \approx 2 d_{m o d e l} n_{l a y e r} (2 d_{a t t n} + d_{f f}) = 12 n_{l a y e r} d_{m o d e l}^{2}$
Dataset size $D$ in tokens
Compute $C \approx 6 N B S$ , where $N$ is model size, $B$ is batch size, and $S$ is number of training steps

Power laws:
- Performance depends strongly on scale (N, D, C), weakly on model shape
- When not bottlenecked, power-law relationship spans over six orders of magnitude
Overfitting:
- Performance enters regime of diminish returns when either $N$ or $D$ is fixed while other increases
- Pentaly ratio of $\frac{N^{0.74}}{D}$ , so scaling model size is slightly less efficient than data size
Efficiency:
- Large models require fewer optimization steps and data points to reach the same performance compared to smaller models
- When using a fixed compute budget $C$ , obtain best performance training very large models without reaching convergence
  - Data requirements grow slowly with compute, $D \sim C^{0.27}$

Since the scalings are power-laws, this means there are diminishing returns as scale increases
The sample-efficiency of large models is surprising and may suggest that “big models” is more important than “big data” moving forward
Using networks that grow as they train might be useful for remaining compute-efficient in settings were data grows, e.g. lifelong/continual learning
Would architecture differences have a greater effect if they weren’t just limited to depth/width scaling of a specific class of architectures (e.g. Transformers)?