Compositional Video Prediction
Ye et al., 2019
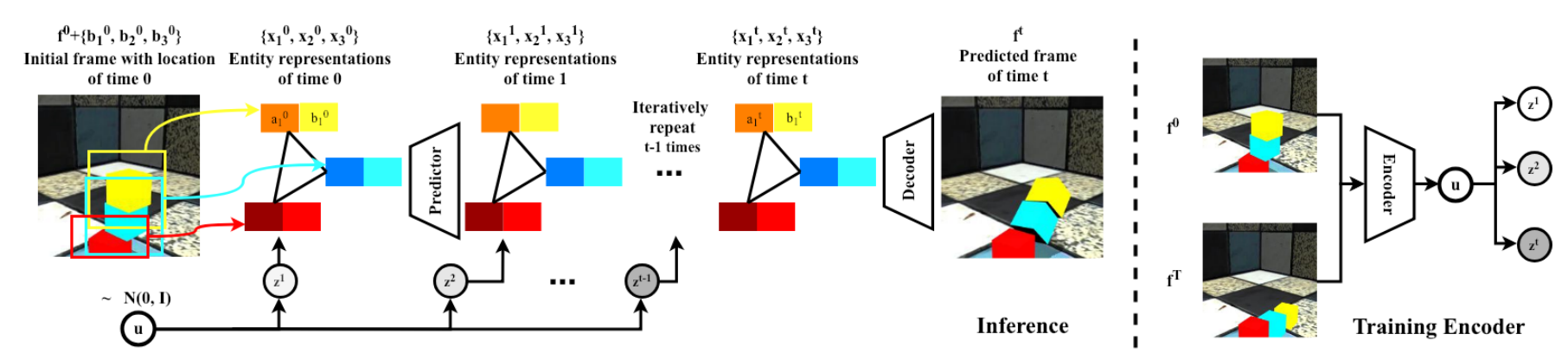 Source: Ye et al., 2019
Source: Ye et al., 2019Summary
- Method for solving pixel-level future prediction given a single image
- Decompose scene into distinct entities that undergo motion and possibly interact
- Generates realistic predictions for stacked objects and human activities in gyms
- Links: [ website ] [ pdf ]
Background
- Given a single image, humans can easily understand the scene and make predictions
- Many other works also model relationships between objects, but do some combination of:
- Use only simple visual stimuli
- Use state based input
- Rely on sequence of inputs
- Don’t make predictions in pixel space
Methods
- Given starting frame
- Use entity predictor
- Interaction between entities modeled with graph neural network, edges are predetermined
- Use frame decoder
- Warp normalized spatial representation to image coordinates with predicted location for each entity
- Use soft masking for each entity to account for possible occlusions
- Add these masked features to features from initial frame
- Single random latent variable
- Yields per-timestep latent variables
- Yields per-timestep latent variables
- Loss consists of three terms:
- Prediction:
- Encoder: information bottleneck on latent variable distribution
- Decoder:
- Prediction:
Results
- Datasets:
- ShapeStacks: synthetic dataset of stacked objects that fall, different block shapes/colors and configurations
- Penn Action: real video dataset of people playing indoor/outdoor sports, annotated with joint locations
- Use gym activities subset: less camera motion, more similar backgrounds
- Metrics:
- Average MSE for entity locations
- Learned Perceptual Image Patch Similarity (LPIPS) for generated frames
- Due to stochasticity from random variable
- Baselines:
- No-Factor: only predicts at the level of frames
- No-Edge: no interaction among entities
- Pose Knows: also predicts poses as intermediate representation, predicts location but not appearance, no interactions
- Proposed method consistenly performs better than the simple baselines on ShapeStacks, but No-Edge is a fairly close second
- Adding adversarial loss, from Pose Knows, greatly improves performance of proposed method on Penn Action
- Qualitative results on Penn Action are generally not that convincing for any model
Conclusion
- Relies on supervision of entity locations and graph structure
- Inclusion of latent variable to model multi-modality is interesting
- Better metrics for evaluating diversity and accuracy would be useful
- Poor performance on real world dataset suggests there is still a lot of room for improvement